http://rredc.nrel.gov/solar/spectra/am1.5/
This is the standard spectrum, at 1000 W/m^2 irradiance, used in the testing of solar energy devices -- namely photovoltaic panels. It could also be useful for modeling the spectrally selective materials used for solar thermal applications. They provide the data in a number of formats for modeling purposes. I'm probably the only person interested in this stuff but there it is, nonetheless. An entire report on the atmospheric physics used for the model is available here:
http://rredc.nrel.gov/solar/models/SMARTS/relatedrefs/SMARTS2_report.pdf
ETR appears to be the extra-terresterial radiation (totals to 1356 W/m2), tilt is a surface at 48.81o to the horizon (total 1000 W/m2). The Tilt numbers are what you would normally apply to a PV cell to determine its peak power output. The direct and circumsolar irradiance appears to be the irradiance on a horizontal surface directly illuminated plus the diffuse light that is scattered off a 'clear' atmosphere (total 887.65 W/m2). I'm not really sure however because the two data sets don't seem to be consistant. Here's a plot of the tilt data, showing the Si exciton peak at 1.12 eV = 1107 nm:
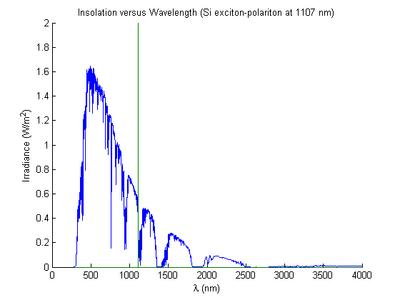Silicon can't absorb the light to the right of the green line -- it doesn't have enough energy to push an electron from the valence band to the conduction band. It's only 148.7 W/m2 lost however. Silicon can absorb light to the left, but only in 1.1 eV chunks. High energy photons (E > 2.2 eV) can actually generate more than one exciton, however. If we look at the actual number of photons per wavelength we get the following:
If we assume every photon with a wavelength below 1107 nm can create one (and only one) 1.1 eV exciton-polariton then the maximum power a Si-photovoltaic cell can absorb is 451 W/m2, or 45 % efficiency. Some people may recognize this as the classic Shockley result, although I derived it numerically in about 15 minutes. With current commercial Si cells running around 12 - 14 % efficiency, you can see that there is a long way to improve even with this most basic design. The actual theorectical (entropy) limits for a solar device are about 95 %. No one is going to get there but it does show you the great potential in solar power, even if it is overly expensive at the moment.
3 comments:
Excellent analysis! The AM1.5 spectrum and I are old buddies, and I've spent many an hour tinkering with it myself.
Just a few things to add: Circumsolar radiation is the radiation that comes from the part of the sky around the sun. This is included with direct radiation because for practical purposes, it is just as good as direct radiation (i.e., it's traveling in the same direction as the direct radiation). Direct + diffuse = global radiation.
Second, while your calculation of the theoretical efficiency limit agrees with Shockley and is correct on the basis of spectral content alone, the actual theoretical maximum efficiency for a single-junction silicon cell is more like 29%. A number of additional factors related to fundamental physical properties of silicon come into play.
Finally, a note on terminology: Excitons and electron-hole pairs are not equivalent. Excitons consist of an electron and a hole that are bound together by the Coulomb force and behave, more or less, as a single particle. Electron-hole pairs also consist of an electron and a hole, but they are not bound to one another and behave as individual particles. While excitons can occur in silicon, they are almost always dissociated into an electron-hole pair by thermal energy (except at extremely low temperatures). Excitons are quite important in some devices, though, such as organic solar cells.
Sorry if I came across as pedantic, but based on previous conversations I figured that you are someone who would appreciate the information.
Marvelous job,
The solar Irradiance and testing on module temperature of pv both are diffrent when climatic conditions/temperature more than 25C to 30C (C=Centigrade).
so clear me if i m wrong.
by mohit
INDIA
"I'm not really sure however because the two data sets don't seem to be consistant."
They are actually consistent, but there are subtleties you might have overlooked.
There are in fact _two_ standard spectra, as described in ASTM G173: the one you describe first is the global irradiance spectrum for a 37deg-tilted surface. It is used for flat-plate PV rating.
These spectra are mutually consistent, and have been generated by my SMARTS spectral model, v2.9.2. See http://www.solarconsultingservices.com/smarts.php
The other one is a direct irradiance spectrum, for direct irradiance at normal incidence. Both are obtained for an air mass of 1.5 and "standard" atmospheric conditions at sea level. The conditions simulated are those typical of the southwest USA, where the atmosphere is very clear (low aerosols, no haze, high solar resource...) This direct spectrum includes a small contribution due to the circumsolar diffuse component within an annulus 3deg from the sun center, which corresponds to the typical field of view of pyrlheliometers. Most of this (small, <1%) contribution cannot be concentrated--contrarily to what Alan says--because the field of view of concentrators used in CPV or CSP applications is much smaller (<1deg). The standard DNI spectrum, including the circumsolar contribution, integrates to 900 W/m2.
The consistency you're after results from the fact that
Global=DNI*cos(zenith angle)+Diffuse
For an air mass of 1.5, the sun's zenith angle is 48.2deg.
Post a Comment